Метод Монте Карло
Общие сведения
Рассмотрим один из примеров применения метода. При
программировании большого и сложного алгоритма управления выводом космического
объекта на орбиту Марса учитываются тысячи различных параметров. Например,
необходимо учитывать изменение массы объекта в связи с расходованием топлива,
изменение силы тяготения, как функции расстояния до космических тел, множество
других важных параметров. Каждый из параметров имеет определенный диапазон
изменения своей величины. Как будет вести себя алгоритм при различных
сочетаниях значений параметров? Перебор всех сочетаний практически невозможен,
так как требует очень много времени. Один из вариантов решения задачи проверки
алгоритма на работоспособность заключается в «набрасывании» в программу
значений параметров с помощью датчиков случайных чисел. Такой способ проверки
основан на методе Монте-Карло.
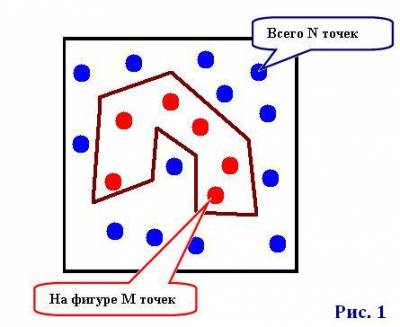
Определение площадей фигур методом Монте-Карло
Идея метода заключается в следующем. Фигуру, площадь которой
требуется определить, помещают в фигуру, площадь которой заранее известна,
например, в квадрат. После этого в квадрат набрасывают точки со случайными
координатами. При этом ведут счет всех точек (k1) и счет точек, попавших в исследуемую
фигуру (k2). Если
обозначить площадь квадрата s1,
а площадь фигуры s2, то
при большом числе всех точек справедливо равенство s2/s1=k2/k1, откуда s2=s1*k2/k1.
В следующих задачах точки со случайными координатами набрасываются
в квадрат размером 200 х 200. Всего точек 40000.
Но уже при набрасывании 1000 точек они достаточно плотно и
равномерно покрывают всю площадь квадрата. На этом и основан метод тестирования
программ и определения площадей фигур.
Ниже показана программа 10.2 определения площади круга. (скачать программу на basic)
RЕМ Метод
Монте-Карло
CLS
a$=
"Метод Монте-Карло, определение площади круга": РRINT
а$
INРUТ "Введите радиус круга
г<100"; r
INРUТ "Введите число точек k1<1"; k1
RANDOMIZE
TIMER
SCREEN 12
PRINT а$
LINE (200,
200)-(400, 400), 14, B ‘квадрат
CIRCLE
(300, 300), г, 14 ‘круг
PRINT
"число точек = ";
FOR i = 1
TO k1
x = INT(RND*200+200): y = INT(RND*200+200)
PSET (x, y), 14 ‘набрасывание случайных
точек
IF
SQR((x-300)^2+(y—300)^2)< = r THEN
k2=k2+1: PSET(x,y) ‘точки, попадающие в круг
END IF
IF i MOD
1000 = 0 THEN PRINT i;
NEXT: PRINT
PRINT
"Всего точек: k1 = ";
k1
PRINT
"Число точек внутри круга: k2
= "; k2
PRINT
"отношение k1/k2 = "; k2/k1
S1 = 200^2:
PRINT "Площадь квадрата: S1
="; S1
S2 =
S1*k2/k1: PRINT "Площадь круга: S2 =
S1*k2/k1 = "; S2
PRINT
"Величина рi = "; S2/(r^2)
PRINT
"Площадь круга, вычисленная по формуле рi*г^2 = " ; 3.14*r^2
END
При запуске программ на исполнение следует обратить внимание
на то, что точность определения площади зависит от количества набрасываемых
точек. Чем больше точек, тем выше точность.
Важным моментом записи программ определения площади фигур
методом Монте-Карло является запись выражений, ограничивающих площадь
исследуемой фигуры. Система ограничений может быть простой, как в случае с
кругом или достаточно сложной при вычислении площадей многоугольников,
криволинейных фигур.
При вычислении методом Монте-Карло площади треугольника
потребуется, например, следующая система ограничений (показана с частью хз, у программы). Она требует определенного положения вершин
треугольника (рис. 2).
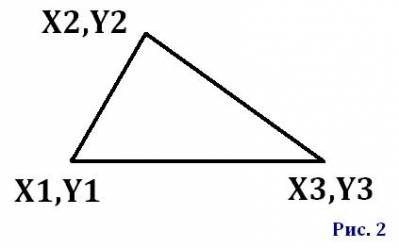
При желании ввести произвольное положение вершин может
понадобиться изменение системы ограничений.
FOR i =
1 TO n ‘ НАБРАСЫВАНИЕ ТОЧЕК В
КВАДРАТ
x = INT(RND*200 +200): y = INT(RND*200
+200) ‘ КООРД. ТОЧЕК
z1 = y>y1+(x-x1)*(y2-y1)/(x2-x1)
z2 = y>y2+(x-x2)*(y3-y2)/(x3-x2)
z3 = y<y3+(x-x3)*(y1-y3)/(x1-x3)
PSET (x,y), 12
IF z1 AND z2 AND z3 THEN
k=k+1: PSET (x,y) ‘ТОЧКИ В ТРЕУГОЛЬНИКЕ БЕЛОГО ЦВЕТА
END IF
NEXT
Есипов А. С. /Информатика. Учебник по базовому курсу// СПб: Наука
и Техника, 2001г. – 384с.
Бейсик - диалоговый учебный язык программирования для персональных
компьютеров. Здесь представлена версия QBasic 4.5
Примеры в электронных таблицах http://www.hcxl.ru/bookQMM04.html#g9t02











